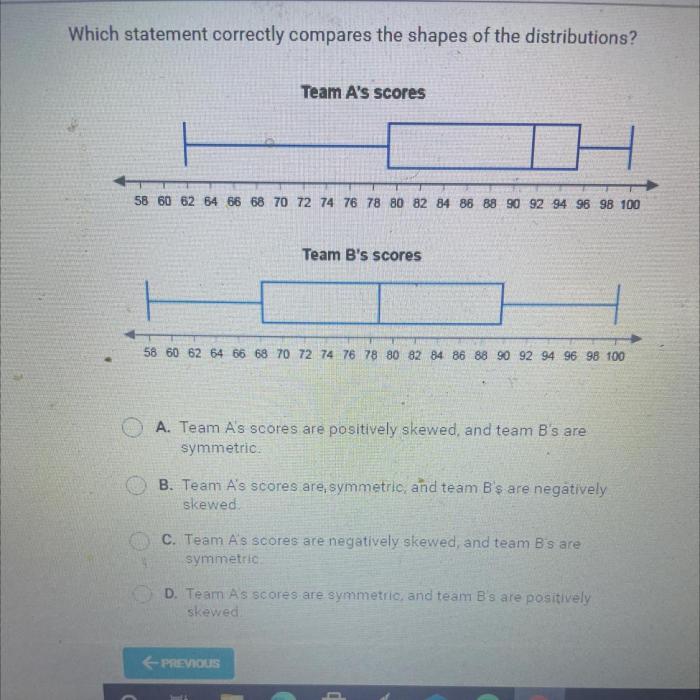
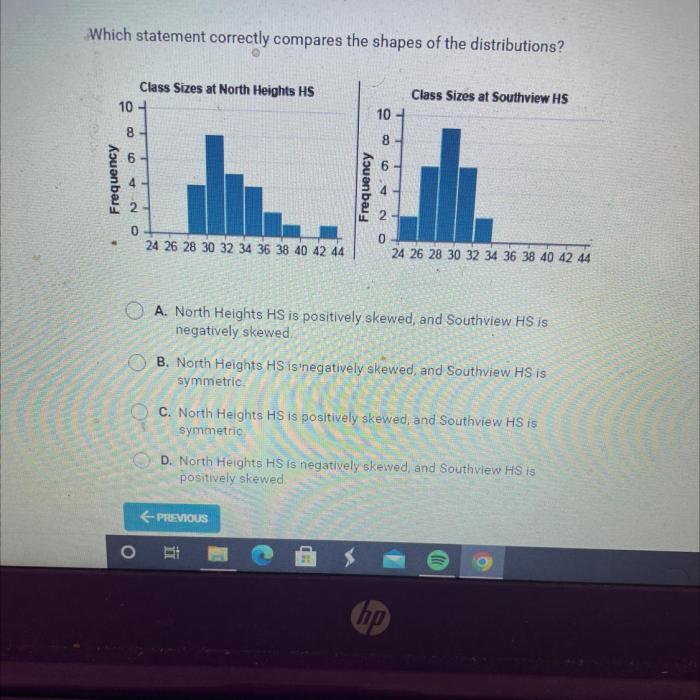
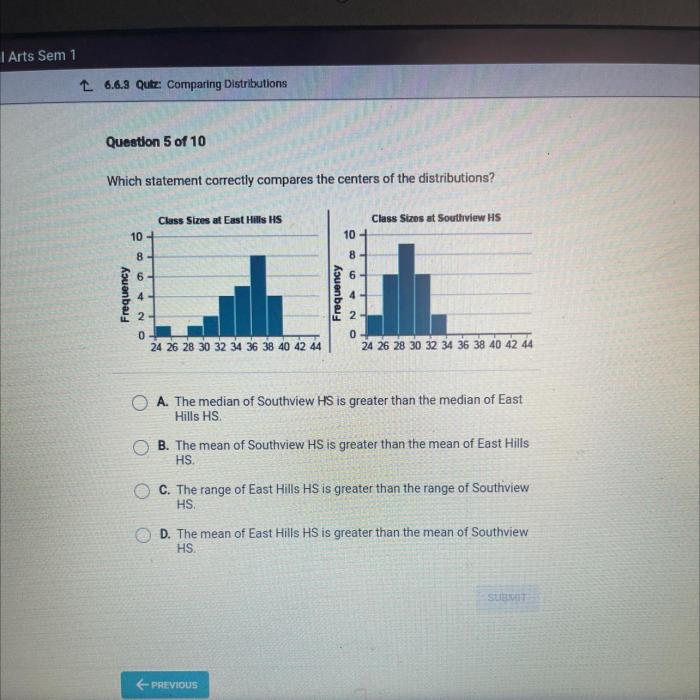
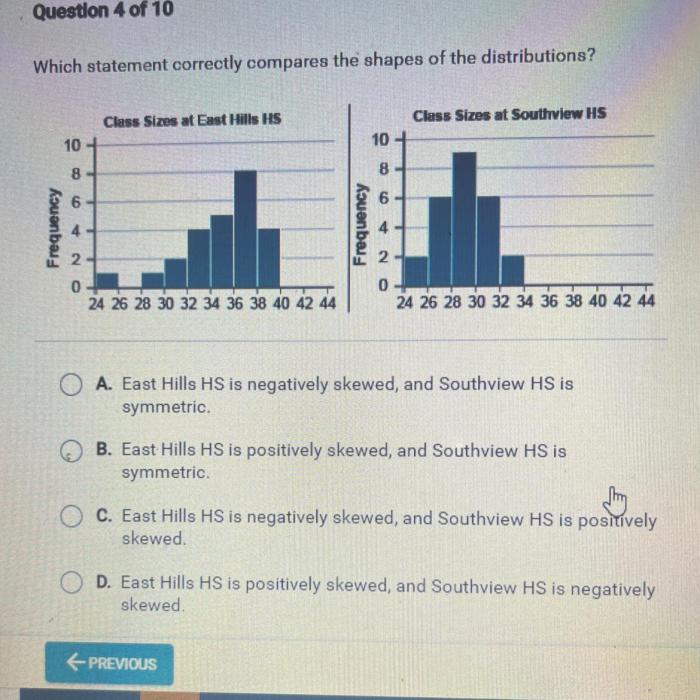
Which statement correctly compares the shapes of the distributions – Which statement correctly compares the shapes of distributions? This question delves into the realm of statistical analysis, where understanding the characteristics of different distributions is crucial for drawing meaningful conclusions from data. This article will explore the concept of distribution shapes, methods for comparing them, and their significance in various fields.
Distributions, often represented graphically, provide valuable insights into the spread and central tendency of data. Different types of distributions, such as normal, skewed, and uniform distributions, exhibit distinct shapes that can reveal important information about the underlying data-generating process.
Analyze the Shapes of Distributions
In statistics, a distribution is a mathematical function that describes the probabilities of occurrence of different possible values for a random variable. The shape of a distribution provides insights into the characteristics of the data it represents. Common distribution shapes include normal, skewed, and uniform distributions.
Normal distributions are bell-shaped and symmetrical around the mean. Skewed distributions are asymmetrical, with one tail longer than the other. Uniform distributions are flat, indicating that all values within the range are equally likely.
Comparison of Distribution Shapes, Which statement correctly compares the shapes of the distributions
Comparing distribution shapes helps identify similarities and differences in data sets. Visual inspection can reveal obvious differences, such as skewness or kurtosis. Statistical tests, such as the Kolmogorov-Smirnov test, can provide quantitative measures of shape differences.
| Distribution Shape | Key Characteristics |
|---|---|
| Normal | Symmetrical, bell-shaped |
| Skewed | Asymmetrical, with one tail longer than the other |
| Uniform | Flat, all values equally likely |
Top FAQs: Which Statement Correctly Compares The Shapes Of The Distributions
What is the purpose of comparing distribution shapes?
Comparing distribution shapes helps researchers understand the underlying patterns and characteristics of data, make inferences about populations, and draw meaningful conclusions from statistical analysis.
What are the different methods for comparing distribution shapes?
Common methods for comparing distribution shapes include visual inspection, statistical tests (e.g., Kolmogorov-Smirnov test), and measures of central tendency and dispersion.
How can distribution shape analysis be applied in real-world scenarios?
Distribution shape analysis finds applications in various fields, including finance, healthcare, and social sciences. It helps researchers make informed decisions, forecast trends, and develop data-driven strategies.